Conjugated Polymer Actuators

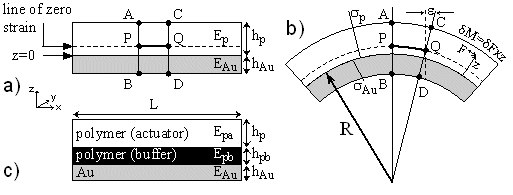
Modeling Bilayer Behavior

Modeling Inplane Strain | Modeling the Bending of Trilayers

With Benjamin Shapiro, we have been working to understand actuator bending.

Modeling Inplane Strain

Timoshenko’s model for bilayer bending due to differences in coefficients of thermal expansion [S. Timoshenko, "Analysis of bi-metal thermostats," J. Opt. Soc. Am., 11, 233-256 (1925)] provides a good starting point for an analysis of actuator bending. For constant moduli and CTEs, the curvature  can be written

where the are the actuation strains, m = h₁/h₂, the hi are the layer thicknesses, n = E₁/E₂, and the Ei are the Young’s moduli. This is valid for small curvatures and assumes a constant actuation strain in the material. Using it thus requires a knowledge of the Young’s moduli of both bilayer materials and their thicknesses. This model also assumes that the stress and strain are related by the modulus and that they are isotropic in the x and y (inplane) directions, and that curvature along the width of the hinge can be neglected.

It should be noted that there is an optimum thickness ratio, given E₁ and E₂. When plotting the curvature versus the thickness ratio m, there is a peak that arises from trading off a higher force due to adding electroactive material and making bending harder by making the beam thicker. This will be true regardless of the two materials, and actuator designers should bear this optimum in mind. For PPy(DBS)/Au bilayers, the optimum thickness ratio was ~5:1, and this changes only slightly with total bilayer thickness. At this ratio, a radius of curvature of only 2 µm was achieved with an Au layer of 500 Å.

It should also be noted that the actuation strain is not the same as the bending strain. The actuation strain is the amount that the actuator “wants” to expand/contract in the plane of the film in the absence of the other layer. How much it is strained due to bending depends on the other layer and the layer thicknesses.

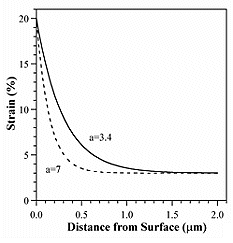
The actuation strain of PPy is, unfortunately, not constant throughout the thickness of the material (z-direction), which is especially notable in thin films. In the bulk, the inplane strain is ~3%. By examining the bending of a large number of bilayer microactuators with different m = h₁/h₂, and modeling the bending by taking into account the possibility of a strain gradient in the PPy film, we found that the strain at the electrolyte/PPy interface is ~17%, and that it decreases to 3% over a distance of ~1 µm.

The figure on the left illustrates the dependence of strain with distance from the electrolyte surface for two different model parameters.

Modeling the Bending of Trilayers

Large interfacial stresses at the polymer/electrode interface caused by repeated expansion and contraction of the polymer during actuation sooner or later result in adhesive failure. Delamination can be improved by roughening the polymer/electrode interface, as shown here link to Preventing Delamination section. Another approach to preventing delamination is to use a “buffer layer” between the polymer and the electrode. By optimizing the thickness and modulus of this layer, the stress at that interface can be reduced to zero, with no loss of curvature and only a small loss in force. For PPy(DBS) 450 nm thick on Au, this ideal intermediate layer should be 150 nm thick and have a modulus of 5 GPa.

Figure from B. Shapiro and E. Smela,
"Bending actuators with maximum curvature and force and zero interfacial stress,"
J. Intell. Mater. Syst. Struct., 18 (2), 181-186 (2006).

For further information see:

• M. Christophersen, B. Shapiro, and E. Smela, "Characterization and modeling of PPy bilayer microactuators. Part 1: Curvature," Sens. Act. B, 115, 596-609 (2006).
• B. Shapiro and E. Smela, "Bending actuators with maximum curvature and force and zero interfacial stress," J. Intell. Mater. Syst. Struct., 18 (2), 181-186 (2006).