Conjugated Polymer Actuators

PANi Fiber Actuators

Santa Fe Science and Technology  |   Polyaniline  |   Fiber Actuators  |   References for Further Information

Santa Fe Science and Technology, Inc.

The research discussed here was done while I was at Santa Fe Science and Technology, Inc. in Santa Fe, New Mexico. The president of SFST is Dr. Benjamin R. Mattes (pdf file).

Polyaniline
The chemical structure of polyaniline is shown here:

Figure from E. Smela, W. Lu, and B. R. Mattes, "Polyaniline Actuators, Part 1: PANI(AMPS) in HCl," Synth. Met., 151 (1), 25–42 (2005).

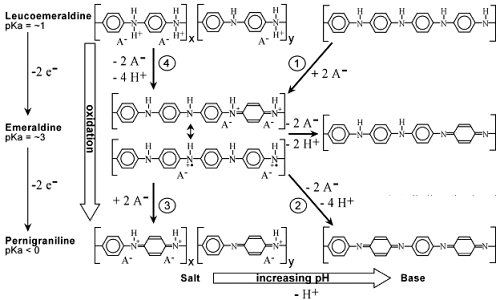
While PPy has two electrochemical states (oxidized and reduced), polyaniline (PANi) has three: leucoemeraldine, emeraldine, and pernigraniline. Not only are ions exchanged, but in aqueous electrolytes there is also proton exchange, since the different states have difference pKa. In water PANi is thus considerably more complex to use for actuators, since oxidation can result in either an expansion or a contraction, depending on pH. A “map” of the ion exchanges, and thus of the actuation is shown below. Polyaniline is electroactive below pH 4, and thus cannot be used for most biomedical applications. When cycled on organic electrolytes, including in ionic liquids, however, the volume increases monotonically with oxidation level, and the actuators are well behaved.

Fiber Actuators

From a processing point of view, PANi has one significant advantage over PPy: it can be chemically synthesized, dissolved in a solvent like NMP, and then either spun into fibers or cast into films – it does not have to be electrochemically deposited to make actuators. An actuator comprising a small-diameter solid PANi fiber separated from a larger-diameter hollow fiber is shown below. Between the two fibers is a gel electrolyte. In this configuration, the outer fiber serves as the counter-electrode link to electrochemistry page, and the inner one as the working electrode, which changes volume upon redox cycling.

Figure from W. Lu, E. Smela, P. Adams, G. Zuccarello, and B. R. Mattes, "Development of solid-in-hollow electrochemical linear actuators using highly conductive polyaniline," Chem. Mater., 16 (9), 1615-1621 (2004)

References for Further Information

• W. Lu, E. Smela, and B. R. Mattes, "Electrochemical actuation of gilded polyaniline bilayers in aqueous acid solutions," Proc. SPIE's 8th Int. Symp. Smart Struc. Mater., Electroactive Polymer Actuators and Devices (EAPAD), Newport Beach, CA, vol. 4329, edited by Y. Bar-Cohen, p. 505-515 (5-8 March, 2001).
• W. Lu, A. G. Fadeev, B. H. Qi, E. Smela, B. R. Mattes, J. Ding, G. M. Spinks, J. Mazurkiewicz, D. Z. Zhou, G. G. Wallace, D. R. MacFarlane, S. A. Forsyth, and M. Forsyth, "Use of ionic liquids for pi-conjugated polymer electrochemical devices," Science, 297 (5583), 983-987 (2002).
• W. Lu, E. Smela, P. Adams, G. Zuccarello, and B. R. Mattes, "Development of solid-in-hollow electrochemical linear actuators using highly conductive polyaniline," Chem. Mater., 16 (9), 1615-1621 (2004).
• E. Smela, W. Lu, and B. R. Mattes, "Polyaniline Actuators, Part 1: PANI(AMPS) in HCl," Synth. Met., 151 (1), 25–42 (2005).
• E. Smela and B. R. Mattes, "Polyaniline Actuators, Part 2: PANI(AMPS) in MSA," Synth. Met., 151, 43-48 (2005).